[미적분학]극한의 엄밀한 정의
이번에 정리할 내용은 극한의 엄밀한 정의를 살펴보고자 합니다. 우리는 고등학교 때, 극한의 정의를 대략적으로 배웠습니다.

그래서 고등학생 때에는 무리 없이 사용했습니다. 하지만 이는 명확한 정의가 아닙니다. 이유는 특정값에 접근할 때, L에 가까워진다. 에서 가까워짐이란 단어가 정확히 어느정도 가까워지는지에 대해 기준이 없기 때문입니다. 그래서 우리는 이러한 명확하지 못한 '가까워진다'라는 단어를 바꾸어서 표현하려 합니다.
1. 극한?
위에서 표현한 방식이 틀린 말은 아닙니다. 극한의 원래 사용은 특정 값에 가깝게 가면(x에서), 어떤 값(y의 값)으로 다가가는 것이 맞는 표현입니다. 극한을 사용한 이유도

실제로 이 함수에 대해 그래프를 그려보면 다음의 그림과 같다.

함수가 초기 상태에서 정의역을 결정하기 때문에, 정의역 값에서 2가 빠져있는 것이다. 그에 따라 y의 값인 3이 빠져야 하는 것이다. 그런데 위의 그래프를 보면, x=2일 때, y=3임이 분명해보인다. 그래서 (2,f(2) = 3)의 값을 표시하고 싶은데, 함수의 정의에 따르면 이를 수학적 기호로 표시하기 어렵다.

그래서 정확히 f(2)의 값은 없지만 그곳에 가깝게 가면 f(2) = 3이 되는 값을 표현하기 위해 극한을 정의하게 된 것이다.
이제 극한을 사용하는 이유에 대해 간략하게 살펴보았으니, 예시를 통해 엄밀한 정의를 정의해보도록 하자.
우리의 예시는

를 가지고 설명해보도록 합시다. 일단 이 극한의 답은 5라는 사실을 알고 있다.
2. 거리를 절댓값으로 정의하자.
절댓값은 거리를 표시하기 위한 기호이다. 그러므로 우리도 절댓값으로 구해보도록 하자. 일단 x가 2에 접근할 때, 그에 따른 함숫값인 f(x)는 어떤 값에 가까워지는지를 수식으로 표시해보도록 하자.
그렇다면 가깝다는 표현대신에 실제적인 수치를 통해 살펴보도록 하자. 가깝다고 하니 인간이 느끼기에 가까워지는 값인 0.1 정도로 생각해보자.
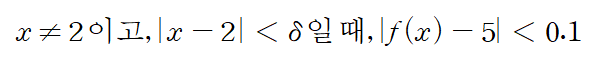
이러한 상태를 갖는다. 여기서 사용된 기호는

으로 사용된다. 여기서 위의 식을 만족하는 델타를 찾는 것이 목표인 것이다. 그런데 우리는 x=2일 때의 값을 원하는 것이 아니기 때문에 x=2가 되는 형태는 피해야 한다. 그래서 위의 식에서 x = 2일 때를 빼야 한다. 물론 x는 2가 아니란 말이 있지만, 말이 길어진다. 그래서 하나의 수식으로 표현하기 위해서 수식을 조금 변경해보자.

로 바꿔볼 수 있겠다. 이를 한 눈에 보기 쉽게 그래프로 생각해보도록 하자..
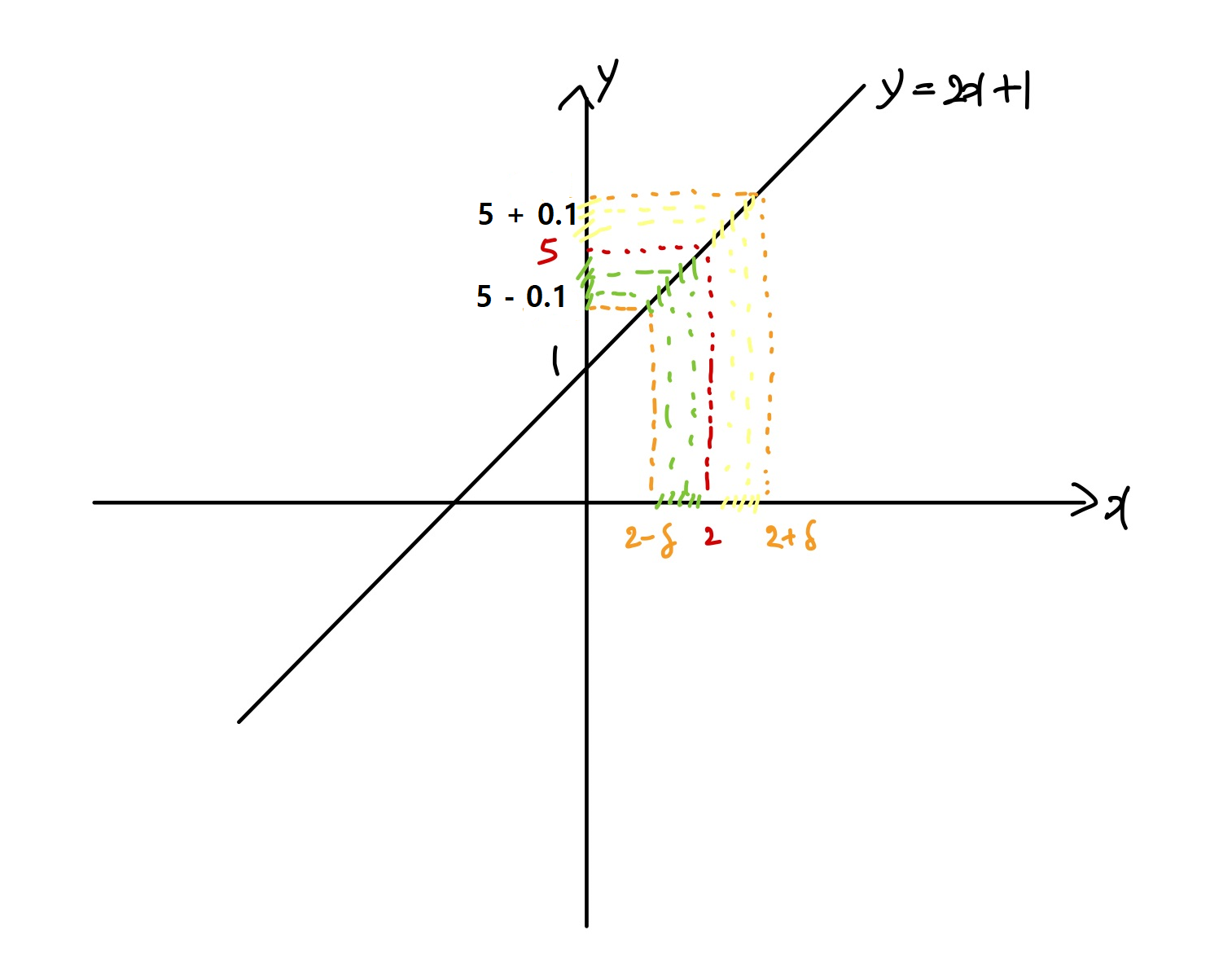
이런 느낌으로 사용할 수 있을 것이다. 그렇다면 이를 만족하는 델타를 구해보도록 하자.

이런 느낌으로 써볼 수 있을 것이다. 우리는 델타를 추정한 것이다. 이를 바탕으로 검증해보면,

이 될 것이다. 이를 계속해서 같은 방식에 따라 늘려가도 비슷한 값이 계속해서 나올 것이다.

이렇게 나올 것이며, 마찬가지로

이러한 형태를 갖게 된다. 그러면 이렇게 수를 계속해서 줄여나가면 언젠가는 엄청나게 작은 값을 가지는 값에 따라 y의 값도 특정 값에 가깝게 갈 것이다. 이를 델타와 입실론을 활용해서 써보면 될 것이다.
3. 그리고 입실론 델타 용법으로 표현

이러한 값을 갖게 되며, 위와 마찬가지로 결론을 내릴 수 있다.

절댓값의 성질에 따라 풀어준 뒤 그래프로 표현해보도록 하자.

이런 느낌의 그래프를 사용할 수 있을 것이다.
말로 표현하면,

이를 통해 극한의 엄밀한 정의를 이야기하면,

여기서 A가 거꾸로 뒤집힌 문자는 For all (모든)을 의미하며, E가 좌우가 바뀐 문자는 Exist(존재하면, 혹은 어떤)이라는 의미한다.
위의 말은 우리가 고등학교 때 배운 말로 바꾸자면, x가 특정 a에 가깝게 가면( 이를 다르게 표현하면 x와 a 사이의 거리를 충분히 가깝게 하면) f(x)와 L의 거리를 임의로 작게 만들 수 있음을 말한다.